Root Calculator

Need to find roots of any degree? Our Root Calculator handles square roots, cube roots, and beyond! Just enter your number and root value for instant, accurate results.

Share Calculator

What is the Root of a Number?

The cube root (n = 3) and square root (n = 2) are the most popular and straightforward root functions. Calculations involving angles employ the cube root. In probability theory, mathematics, geometry, physics, and statistics, the former is very useful. A value that equals the original number after being multiplied by itself n times is known as the root of a number, or more precisely, the nth root. The most typical roots are:
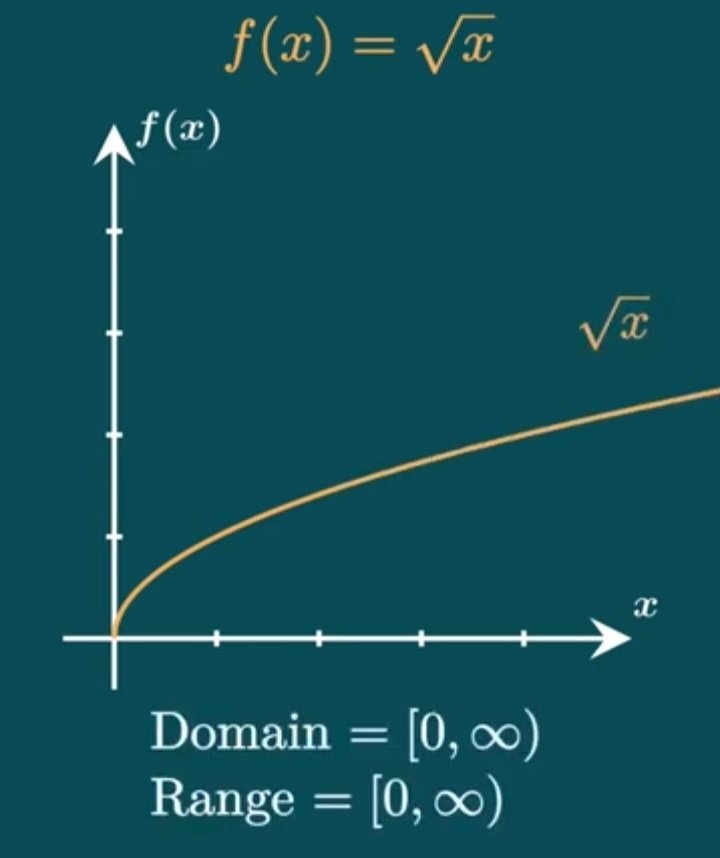
The square root, denoted by √, is the number's second root (n = 2). As stated otherwise, the value is multiplied to obtain the initial number. For example, since 4 × 4 = 16, 4 is the square root of 16.
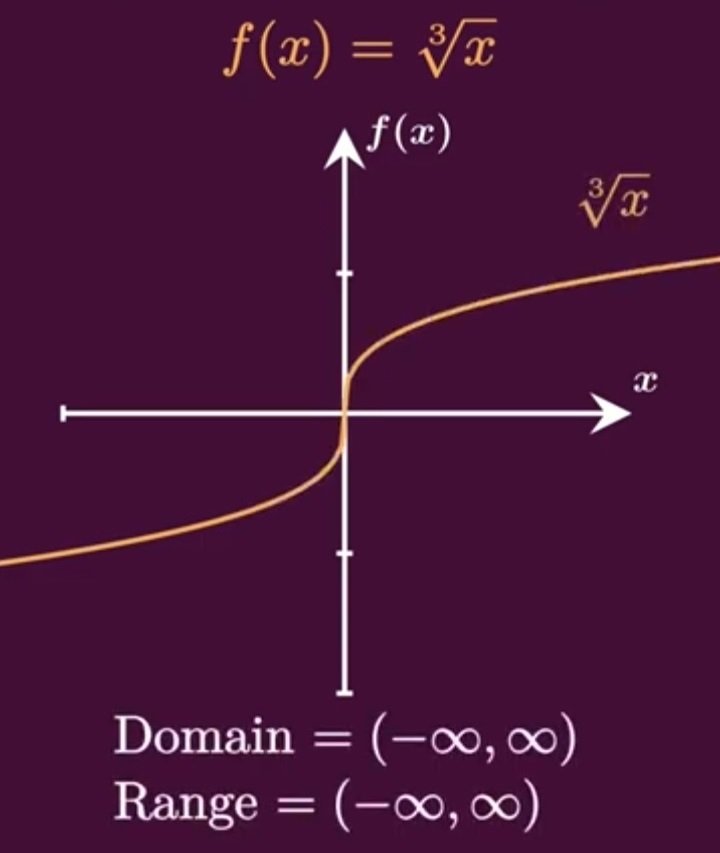
Cube root: the third root (n = 3) of a number, denoted by ³√. To retrieve the original number, multiply the value by itself three times. For instance, since 3 x 3 x 3 = 27, 3 is the cube root of 27.

What does a number's root mean?

The solution to this question is the nth root of a number. "What number can I multiply by n times to get this number?" Since this is the opposite of the exponentiation process, in which the exponent is n, we can say that "r is the nth root of x" if rn = x. The root symbol √ is used specifically in mathematics to denote the process of finding the roots of a number.
If n is even, there are always two roots, one positive and one negative, which have the same value and opposite sign. The principal root is the name given to the positive solution. If n is odd, there is only one real number root with the same sign as x. This is the principal root. While some roots, such as the cube root, can have conjugate and complex number solutions, our root calculator will always find the elementary root.
The most popular root functions are the square root (n = 2) and the cube root (n = 3), the first of which has many uses in probability theory, statistics, physics, geometry, and mathematics. The cube root is used in angular calculations.

Root Calculation Formula

The n^th root of a number x is calculated as:

Where:
x = The number (radicand)
x = The degree of the root

Calculation Examples

Example 1: Square Root (n=2)

Calculate: $\sqrt[2]{25}$

Result: The square root of 25 is 5.

Example 2: Cube Root (n=3)

Calculate: $\sqrt[3]{27}$

Result: The cube root of 27 is 3.

Example 3: Fourth Root (n=4)

Calculate: $\sqrt[4]{16}$

Result: The fourth root of 16 is 2.

Square Root function

The square root and cube root functions for a limited collection of integers are shown here:

Cube Root Function