Antilog Calculator

Need to reverse a logarithmic value? Our Antilog Calculator makes it easy! Whether you're working with pH levels, decibels, or financial growth rates, quickly convert log values back to their original numbers. Just enter your log result and base to get instant antilogarithm solutions.

Share Calculator

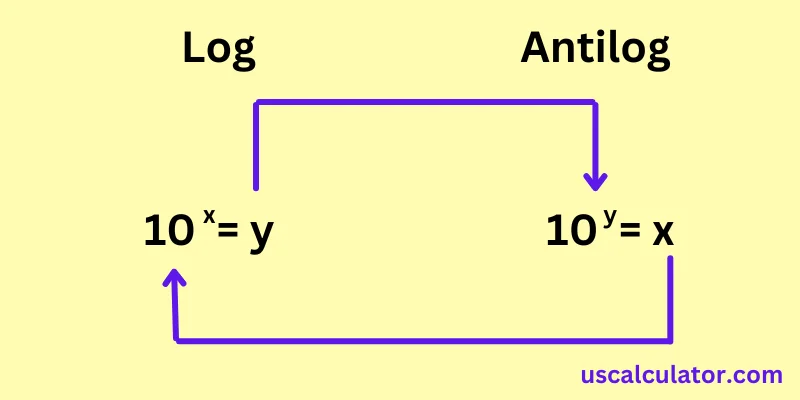
What is a Logarithm?

A logarithm answers the question:
"To what power must we raise a base number to get another number?"
Mathematically:

Where:

• $b$ = Base (must be > 0 and ≠ 1)
• $a$ = Positive number
• $c$ = Logarithm (exponent)

Example
log₁₀ (100) = 2    because 10² = 100

Antilog Calculation Formula

An antilogarithm (antilog) reverses the log process, converting a logarithmic value back to its original number.
Antilog Formula

• $b$ = Original base
• $c$ = Logarithmic value

Antilog Calculation Example

Example 1: Base 10 (Common Antilog)
Find antilog₁₀ (3.5)
Answer
10^3.5 = 3162.28
Used in pH calculations (e.g., converting pH 3.5 back to H⁺ concentration).
Example 2: Base *e* (Natural Antilog)
Find antilog_e (2) (i.e., e²)
e² = 7.389
Used in continuous growth models.
Example 3: Custom Base (Base 2)
Find antilog₂ (5)
Answer
2⁵ = 32
Used in computer science (binary systems).

100 Logarithm Base and Number 5 Antilog Calculation Example with Formula

Now let us understand antilog calculation. The logarithm and the antilogarithm are inverse operations. The antilogarithm with a base of 100 for the logarithm of 5 is calculated using the formula:
Antilog₁₀₀ (log₁₀₀ (5)) = 100^log 100⁽⁵⁾
So, you raise the base (100) to the power of the logarithm of the given number (5) with a base of 100. In this case, since the logarithm is 5, the calculation simplifies to:
Antilog₁₀₀ (5) = 100⁵
Using a calculator:
Antilog₁₀₀ (5) = 100⁵ = 10,000,000,000
Therefore, Antilog₁₀₀ (5) is equal to 10,000,000,000.

How to calculate an antilog?

Here, we understand the antilog and how to calculate the antilog. We will raise the base to that number by exponentiating the supplied log number to determine the antilog of that log number with that base. We will take an example here to calculate the inverse log function.
log₅3 (antilog of 3 with a base of 5), just solve 5³ = 5 x 5 x 5 = 125
Here, we will take the antilog of 2 with a base of 7 as an additional example. To calculate it, raise 7 to the power of 2.
resulting in: 72 = 7 x 7 = 49.
If you calculate antilog according to the antilog calculation formula, but you aren't sure, then use our Antilog calculator to check if your calculation is correct.

Comprehending Antilogarithms: Acquiring Knowledge of the Logarithmic Inverse

If you have never heard of antilog, then antilog, or simply antilog, refers to the inverse value of a logarithm. Antilogarithm is the reverse of log: they generate the exponent you need to raise a base number to a certain value. But they reveal the number that you get when you lift the base to the power of a certain exponent.

Calculating an antilog is straightforward. You can either:

Use a calculator: Most scientific calculators have a dedicated "antilog" button or a function like log^(-1). Just enter the value of the exponent (y) and choose the correct base (b).
To the exponent's power, raise the base: The manual technique is as follows. Antilog_10(2), for instance, is equal to 10 raised to the power of 2, or 100.

Utilising the antilog function in real-world applications

Converting power ratios in electronics and acoustics from decibel (dB) values. Using pH values (negative logarithms of hydrogen ion concentration) to calculate concentrations in chemistry.Modeling physics and biological events with exponential growth or decay.
Coding and cryptography to provide safe data transfer. Numerous disciplines use signal processing and image analysis.