Logarithm Calculator
Struggling with logarithmic calculations? Our Logarithm Calculator simplifies complex math! Whether you're working with natural logs (ln), base 10, or custom bases, get accurate results in seconds. Essential for algebra, chemistry, pH levels, and sound engineering. Just input your values and let our tool do the work.
Share Calculator
Common Calculators | |
Table of Contents
Logarithms: Calculation Formulas & Examples
1. Basic Logarithm Definition
Where:
- = Base (must be > 0 and ≠ 1)
- = Argument (must be > 0)
- = Exponent (the logarithm result)
Example:
log2 (8) = 3 because 23 = 8
2. Common Logarithm (Base 10)
Used in: pH calculations, decibel measurements
Example
log (100) = 2 because 102 = 100
3. Natural Logarithm (Base e)
e = 2.71828 (Euler's number)
Example
ln (20) = 3.0 because e3.0 = 20.1
4. Change of Base Formula
Useful for: Calculating logarithms with uncommon bases
Example:
| log5 (25) = |
|
= |
|
= 2 |
5. Logarithm Properties
| Property | Formula | Example |
|---|---|---|
| Product Rule | ||
| Quotient Rule | ||
| Power Rule | ||
| Logarithm of 1 | ||
| Logarithm of Base |
Calculation Examples
Example 1: Solve for *x* in log4 (x) = 3
43 = x So x = 64
Example 2: Simplify log2 (8) + log 2 (4)
log2 (8 × 4) = log2 (32) = 5
Example 3: Convert log3 (7) to natural logarithms
| log3 (7) = |
|
= |
|
= 1.771 |
100base and number 5 logarithms calculation example
Now, we will learn logarithms and logarithm calculation. For this, we take an example. Calculate the 100 base and number 5 logarithms calculation. Calculate the natural logarithm (loge) of the number 5:
loge(5) = 1.609loge (5) = 1.609
Calculate the natural logarithm (loge) of the base 100:
loge(100)≈4.605loge (100) = 4.605
Divide the result from step 1 by the result from step 2:
| log100 (5) = |
|
= 0.3495 |
So, the correct value for log100 (5) is approximately 0.34950
Common logarithms (base 10). Below is a logarithm table for numbers 1 to 20.
| Number | log10 |
|---|---|
| 1 | 0.0000 |
| 2 | 0.3010 |
| 3 | 0.4771 |
| 4 | 0.6021 |
| 5 | 0.6990 |
| 6 | 0.7782 |
| 7 | 0.8451 |
| 8 | 0.9031 |
| 9 | 0.9542 |
| 10 | 1.0000 |
| 11 | 1.0414 |
| 12 | 1.0792 |
| 13 | 1.1139 |
| 14 | 1.1461 |
| 15 | 1.1761 |
| 16 | 1.2041 |
| 17 | 1.2304 |
| 18 | 1.2553 |
| 19 | 1.2788 |
| 20 | 1.3010 |
The following rule can also be used to modify the logarithm's base.

Apply the following rule to swap the argument and base.
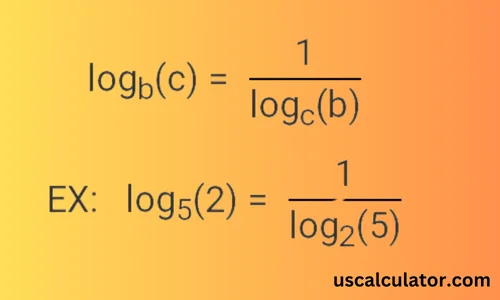
Other typical logarithms to be aware of are:

If you want more information on Logarithm Calculation. So read more .....