Area Calculator

Calculate areas effortlessly with our versatile Area Calculator. Perfect for students, teachers, and professionals, this tool handles squares, rectangles, triangles, circles, and more complex shapes. Get accurate results instantly with easy unit conversion.

Image

Area of

Square Rectangle Triangle Circle Parallelogram Trapezoid Ellipse (Oval) Sector Octagon

Solve triangle by    

Base and Height Three Sides (Heron's formula) Two Sides and Included Angle

Result Unit

mm² cm² dm² m² km² in² ft² yd² mi²

Width

mm cm dm m km in ft yd mi

Length

mm cm dm m km in ft yd mi

Side

mm cm dm m km in ft yd mi

Side b

mm cm dm m km in ft yd mi

Radius

mm cm dm m km in ft yd mi

Minor Radius

mm cm dm m km in ft yd mi

Angle α

°

Height

mm cm dm m km in ft yd mi

Calculate

Results

Area	0 cm²

Share Calculator

What is area?

What is area? The space enclosed by any figure made on a plane is called the area. For example, there is a rectangle and the space enclosed inside it or the area of the whole rectangle is called the area of a triangle. So the space enclosed inside this triangle is called the area of the whole triangle. Similarly, the space enclosed inside a circle is called the area of a circle.

Ever found yourself staring at a wall, trying to guess how much paint you'll need? Or maybe you've planned a garden and wondered how many bags of soil to buy. Perhaps you've been drafted as a math homework helper and needed a quick refresher. In all these moments, you're actually solving a common puzzle: figuring out area.

This is where an Area Calculator swoops in to save the day. Think of it as a handy digital assistant that does the math for you. It gives you quick and accurate answers for a ton of different shapes, saving you time and making sure you get it right. This guide will walk you through the basics of calculating area yourself and show you how an online calculator can make your life a whole lot easier.

Area of a Square: Formulas and Examples

What is a square? A square is a quadrilateral with four sides of equal length and four right angles (90°). It is one of the simplest shapes. And to find its area, only its length needs to be known. The equation for calculating the area of a square is as follows:
Formula: Area = side × side = s²
s = length of one side.
Example
Imagine you are tiling a 5 foot square bathroom floor. This means how many tiles you will need to cover the floor.
Area = 5 ft × 5 ft = 25 ft ².
We have square tiles of 1 ft * 1 ft
Area = 1 ft × 1 ft = Area of 1 foot ² tile.
This means you will need 25 tiles of 1 foot ² to cover a 25 foot ² floor.

Area of a Rectangle: Formulas and Examples

What is a rectangle? A rectangle is a quadrilateral with four right angles and two sides of equal length and two sides of equal width. It is one of the simplest shapes, in the case of a rectangle, the length usually refers to the two longer sides of the quadrilateral, while the width refers to the shorter of the two sides. The equation to find the area of a rectangle is as follows:
Formula: Area = length × width = l × w
l = length, w = width.
Imagine you are tiling a 15 feet long and 10 feet wide room floor. This means how many tiles you will need to cover the floor.
Area = 15 ft × 10 ft = 150 ft ².
We have square tiles of 1 ft * 1 ft
Area = 1 ft × 1 ft = Area of 1 foot ² tile.
This means you will need 150 tiles of 1 foot ² to cover a 150 foot ² floor.
Example: A notebook page measuring 8.5 inches by 11 inches has an area of 8.5 × 11 = 93.5 in². This formula is versatile—use it for rooms, gardens, or even calculating fabric for curtains. Just remember, if it's a square, it's still a rectangle with four right angles (90°) equal length and width!

Area of a Triangle: Formulas and Examples

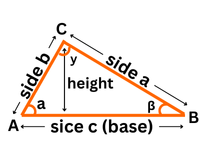
What is a triangle? The shape formed by joining any three points with a line is called a triangle. It has three sides and three angles. Triangles can be complicated to understand and calculate the area because of their three sides and angles, but once you understand them, they seem interesting. The area of a triangle measures the space between those three points. The equation to calculate the area of a triangle is given below
Formula (Standard): Area = ½ × base × height = ½ × b × h
b = length of the base, h = perpendicular height.
For instance, a triangular sail on a boat with a base of 6 meters and height of 4 meters: A = (6 × 4) / 2 = 12 m². Or think of a pizza slice—base 10 cm, height 12 cm: A = (10 × 12) / 2 = 60 cm².
Heron's Formula
There are advanced versions too, like Heron's formula for when you know all sides: A = √[s(s-a)(s-b)(s-c)], where s is the semi-perimeter (a + b + c)/2. Say sides are 3, 4, 5 cm: s = 6, A = √[6(6-3)(6-4)(6-5)] = √[6 × 3 × 2 × 1]=√36=6 cm². Triangles are key in architecture and engineering.

Area of a Circle: Formulas and Examples

What is a circle? A circle is a basic geometric figure that is defined as the set of all points on a plane that are equidistant from a fixed point called the center. The constant distance from the center to any point on the circle is called the radius.
A circle is a perfectly round shape where all points are equidistant from the center. The key to its area is the mathematical constant Pi (π), where π is approximately 3.14159.
Formula: Area = π × radius² = πr²
r = radius (distance from center to edge).
Imagine a round table with a radius of 2 feet: A = 3.1416 × 2² = 12.566 ft². That's how much tablecloth you'd need. For a coin with radius 1 cm: A = π × 1² = 3.14 cm². If you have the diameter (twice the radius), use A = π(d/2)². A circular pizza has a radius of 15 cm. Area = π × (15 cm)² = 3.1416 × 225 = 706.86 cm². Circles are in pizzas, wheels, and even manhole covers grab a calculator for π to keep it precise.

Area of a Parallelogram: Formulas and Examples

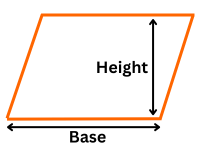
A parallelogram is a quadrilateral (a four-sided polygon) in which both pairs of opposite sides are parallel and equal in length, but angles aren't always right. Its area calculation is similar to that of a rectangle. opposite angles equal, and diagonals that bisect each other. It is a fundamental figure in geometry with wide applications in mathematics and design.
Formula: Area = base × height = b × h
b = length of the base, h = perpendicular height (not the length of the slanted side).
Imagine a slanted fence panel: base 8 feet, height 5 feet, A = 40 square feet. Or a diamond-shaped kite: base 10 cm, height 7 cm, A = 70 square cm. Don't mix up the side length with height; that's a common slip-up. You'll see these in logos or floor patterns.

Area of a Trapezoid: Formulas and Examples

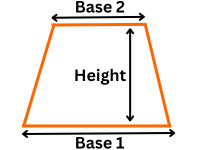
What is a trapezoid? A trapezoid is a four-sided shape with at least one pair of parallel sides. These parallel sides are called the trapezoid bases. while the non-parallel sides are known as the legs. widely used in geometry and real-world applications such as architecture and engineering.
Formula: Area = ½ × (base₁ + base₂) × height = ½ × (a + b) × h
a and b = lengths of the two parallel bases, h = perpendicular height between them.
Imagine for a trapezoid-shaped driveway: tops 15 ft and 10 ft, height 20 ft, A = (15 + 10) × 20 / 2 = 250 square feet. Or a slice of land: 6 m and 4 m parallels, 3 m height, A = (6 + 4) × 3 / 2 = 15 square m. Great for roadsides or tents.

Area of a Ellipse (Oval): Formulas and Examples

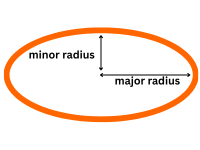
An ellipse looks like a flattened circle and has two radii: a longer semi-major axis and a shorter semi-minor axis. An ellipse (commonly referred to as an "oval") is a closed, symmetric curve in a plane that surrounds two focal points (called foci). It is defined as the set of all points such that the sum of the distances from any point on the curve to the two foci is constant.
Formula: Area = π × semi-major axis × semi-minor axis = π × a × b
a = semi-major axis (longest radius), b = semi-minor axis (shortest radius).
Say an oval table: long axis 10 ft (a = 5), short 6 ft (b = 3), A = 3.14 × 5 × 3 = 47.1 square feet. Or An ellipse has a semi-major axis of 10 cm and a semi-minor axis of 6 cm.Area = π × 10 cm × 6 cm = 3.1416 × 60 = 188.5 cm² These model planets' paths or fancy windows.

Area of a Sector: Formulas and Examples

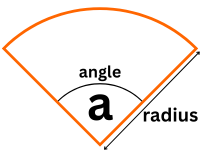
A sector is a portion of a circle bounded by two radii and an arc. It look like a "slice" of a pie or pizza. Its size depends on the radius of the circle and the measure of the central angle. It is widely used in geometry, trigonometry, and data visualization.
Formula: Area = (θ / 360) × πr²
θ = the central angle in degrees, r = radius.
Example
For a 60-degree pie slice, r = 5 cm: A = (60/360) × 3.14 × 25 = (1/6) × 78.5 = 13.08 square cm. Or a 180-degree semicircle fan: half the full area. Sectors are in charts and clocks. Imagine a sector of a circle has a 90° angle and a radius of 8 inches. Area = (90 / 360) × π × (8 in)² = 0.25 × π × 64 = 50.27 in².

Area of a Octagon: Formulas and Examples

An octagon is an eight-sided polygon. An octagon is a polygon with eight sides, eight angles, and eight vertices. When all sides and angles are equal, it is called a regular octagon, known for its symmetry and balanced shape. Octagons are widely used in construction, design, and everyday objects. A common example is a stop sign. The word "octagon" comes from the Greek words 'okto' meaning "eight" and 'gonia' meaning "angle."
Formula (Regular Octagon): Area = 2 × (1 + √2) × s²
s = length of one side.
A regular octagon has a side length of 5 cm.
Area = 2 × (1 + √2) × (5 cm)² = 2 × (1 + 1.414) × 25 = 2 × 2.414 × 25 = 120.7 cm².A regular octagon has a side length of 2 ft.: A = 2(1 + 1.414) × 4 = 2 × 2.414 × 4 = 19.3 square feet.