Area of a Sector Calculator
Need to find a circle sector's area? Our free calculator makes it easy! Just input the radius and angle (degrees or radians) for instant results. Ideal for geometry homework, architectural designs, or DIY projects. No complex math required - get precise sector areas in seconds. Try it now!
Share Calculator
Common Calculators | |
Table of Contents
About Area of a Sector Calculator
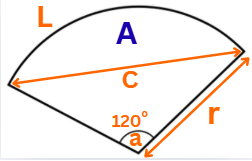
In today's article, we will learn about the area of a sector and the length of an arc. What is the area of the sector, and how can we find its area? First, let us understand what a sector is. We have given the photo below, which has a drawing of the sector. You can understand this example by looking at the drawing of that sector.
A sector is the area enclosed between two radii and an arc. So the sector is the area between two radii and R, as shown in the photo; here A is an arc and P is our radius; the area in between is called the sector. So this portion between radius and R is our sector. The remaining portion here is also a sector. So we will call it a major sector, and the smaller one is our minor sector.
Now, if we want to find the area of a sector, then its formula is that we have Area of a Sector = Theta / 360 × pi r square. Now, what is Theta? The angle formed between these two radii is our theta, and here APB is the arc, so the formula to find it is the length of an arc; its formula will be theta upon 360 × 2 pi r. So these are two formulas. The first formula is to find the area of a sector; okay, the second is to find the length of an arc.
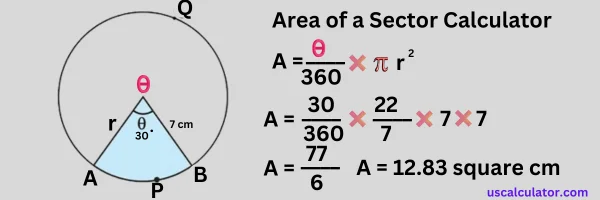
Let's take an example. Find the area of a sector of a circle with a radius of 7 cm and an angle of 30 degrees. So here we have a circle, and a sector is formed in the middle of it whose radius has been given to us, which is 7 cm, and the angle formed between both the radii is 30 degrees, so our r is 7 cm and theta is 30 degrees. So, if we want to find the area of a sector, the formula is the formula of the area of a sector: area = theta / 360 × pi × r². So here we put the value; our r is 30. In our case, 30 / 360 × 5 is 22 / 7, and our radius is 7, so 7 × 7. area = 11 × 7. So if we multiply 11 by 7, it will become 77. Area = 77 / 6. Here, 77 divided by 6 is 12.83 square cm. So this is the area of our sector.

Area of a Sector Formula
Here on this page, we will learn how to size an area and understand how it is calculated. This is very simple and easy. Let's start by understanding what the field is. The area looks like a slice of pizza or like a slice of pie from a full circle. We use Simple to find the location of this field.
Ingredients:
Area of a Sector = (θ/360) × π × r²
If you have not given a radius and you are given a diameter, you can use the formula below. However, it should be remembered that the radius is always half the circumference. And its circumference is always twice the radius. That is, if the radius is 50, the circumference is 100. If the circumference is 60, the radius is 30.
Radius = Diameter / 2
diameter = Radius * 2
A = (θ / 360) × π × r²
Area of a Sector = (angle / 360) x π x (diameter / 2)²
A Area of the sector
θ is the angle of the sector (in degrees).
π is a mathematical constant (approximately 3.14159).
r is the radius of the circle.
When angle is in degrees (°):
| Area = ( |
| ) × πr2 |
| Area = ( |
| ) × θ × r2 |
Calculation Example - Find the Area of a Sector
Find the area of a sector with a radius of 8 cm and a central angle of 60°.
Use the formula for degrees:
| Area = ( |
| ) × π × 82 |
| Area = ( |
| ) × π × 64 = 10.6667 ×3.14159 |
Find the area of a sector with a radius of 6 cm and a central angle of 60°.
Step 1: Use the formula for degrees:
A = (θ / 360) × π × r²
Step 2: Plug in the values:
θ = 60°, r = 6 cm, π ≈ 3.14159
A = (60 / 360) × π × 6²
A = (1/6) × π × 36
A = (36π) / 6
A = 6π ≈ 6 × 3.14159 ≈ 18.8496 cm²
Answer: The area of the sector is approximately 18.85 cm².
FAQ
Q: Which industries can the Area of a Sector calculator be applied to?
A: In fact, the size of the sector does not matter, nor does its central angle, and the calculator can be used for any sector.
Q: What method does the Area of a Sector calculator employ?
A: A Calculator uses the Area of a sector = (central angle/ 360) × π × Radius².
Q: Can we use this Area of a Sector calculator to calculate the area of a circle somehow?
A: You certainly can. As simple as specifying the circle's radius and an angle of 360 degrees.
Q: Is the Area of a Sector calculator precise?
A: However, with the given parameters, the calculator yields precise results and thus is quite efficient.
Q: What shapes can I enter into the Area of a Sector calculator?
A: No, it will not be useful for finding the area of any shape other than sectors because this calculator is designed for this sole purpose.