Perimeter of a Triangle Calculator
Need to find a triangle's perimeter? Our free Perimeter of a Triangle Calculator makes it easy! Just enter the three side lengths, and get your result in seconds. Ideal for geometry homework, construction projects, and design work. Fast, precise, and user-friendly
Share Calculator
Common Calculators | |
Table of Contents
- 1. What is the Perimeter of a Triangle?
- 2. Perimeter of a Triangle Formula
- 3. SSS (Side-Side-Side) Calculation Formula and Calculation
- 4. SAS (Side-Angle-Side) Calculation Formula and Calculation
- 5. SSA (Side-Side-Angle) Formula and Calculation
- 6. ASA (Angle-Side-Angle) Formula and Calculation
- 7. Examples: Calculate a Triangle's Perimeter
What is the Perimeter of a Triangle?
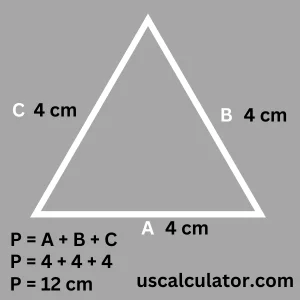
Here we are going to understand the perimeter of a triangle. This is a simple method because you have to apply the formula, which is P = A + B + C. Now what is this? A triangle has three parts (sides), which are A, B, and C. Here, A is 4 cm; after that, we will keep B 4 cm and C 4 cm, which means all three sides are of the same length. What we have to do here is A + B + C. Here we have to add the length of the side of the triangle. Then we will get its perimeter. What is a perimeter? See here that the overall border of the triangle is its border; we call it the perimeter. We can also call it circumference; if it is a circle, then we can also call it its circumference; otherwise, we call it perimeter. So see here what will be our A = 4 cm, B = 4 cm, and C = 4 cm. So what will happen here? 4 + 4 + 4 = 12 cm. Here, the perimeter of the triangle will be 12 cm. An image is given below to understand the example.
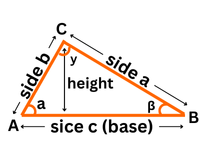
Perimeter of a Triangle Formula
Curious about the distance around a triangle? The Perimeter of a Triangle Calculator is your shortcut. The formula is simple - add up the lengths of all three sides. It's like measuring the edges and joining them up. The formula for the perimeter of a triangle is
P = side a + side b + side c
An image is given below to understand.

SSS (Side-Side-Side) Calculation Formula and Calculation
Calculation Formula - Add up the lengths of all three sides of the triangle.
P SSS = a + b + c
Calculation Example - Here a, b, and c are the lengths of the three sides of the triangle.Let's say we have a triangle with side lengths a = 5, b = 7, and c = 9 units.
P SSS = 5 + 7 + 9 = 21 units
So, the perimeter of the triangle is 21 units.
SAS (Side-Angle-Side) Calculation Formula and Calculation
Calculation Formula - Add the lengths of the two known sides and multiply the sum by 1/2 times the sine of the included angle, then add the length of the remaining side.
P SAS = (a + b) + c ⋅ sin(θ)
Where a and b are the lengths of the known sides, c is the length of the unknown side, and θ is the measure of the included angle.
Calculation Example - Suppose we have a triangle with side lengths a = 6 units, b = 8 units, and an included angle θ = 45∘, and we want to find the length of side c.
c2 = 62 + 82 - 2 × 6 × 8 × cos(45°)
c2 = 36 + 64 - 96 × cos(45°)
c2 = 100 - 96 × 7071...
c2 = 100 - 67.8816... = 32.1184...
c = √32.1184...
c = 5.6673...
c = 5.6673 to 2 decimal places ( length of side c. )
perimeter = A + B + C
perimeter = 6 + 8 + 5.6673 = 19.6673 units.
so, the perimeter of the triangle is approximately 19.6673 units. ( 19.7 units)
SSA (Side-Side-Angle) Formula and Calculation
Calculation Formula - Use the Law of Sines to find the length of one of the unknown sides, then calculate the perimeter using the lengths of all three sides.
P SSA = a + b + c
Calculation Example - Let's say we have a triangle with side lengths a = 5 units, b = 7 units, and an angle a = 30∘, and we want to find the length of side c.
Using the Law of Sines:
|
= |
|
= |
|
| = |
|
Solving for sin(β), we find
| sin (β) = |
|
Since β is an acute angle,
| β = sin-1 |
| or approximately 44.43 ∘. |
Now, using the Law of Sines again to find side c:
| = |
|
Solving for c, we get c = 8.71 units.
Now, calculating the perimeter:
P SSA = 5 + 7 + 8.71
P SSA = 20.71 units
So, the perimeter of the triangle is approximately 20.71 units.
ASA (Angle-Side-Angle) Formula and Calculation
Calculation Formula - This situation uniquely determines a triangle, so the perimeter is simply the sum of all three sides.
P ASA = a + b + c
Calculation Example - Given a triangle with angles a = 30∘, β = 60∘, and side b = 8 units, we can calculate the lengths of sides a and c using the Law of Sines or the Law of Cosines. Once all three sides are known, we can calculate the perimeter straightforwardly as shown in the previous examples.
Examples: Calculate a Triangle's Perimeter
some examples.
Example 1
Side A: 5 units
Side B: 8 units
Side C: 6 units
Using the Perimeter Formula: 5 + 8 + 6 = 19 units
So, the perimeter is 19 units.
Example 2
Side A: 12 cm
Side B: 12 cm
Side C: 12 cm
All sides are equal, making it an equilateral triangle.
Perimeter Formula: 12 + 12 + 12 = 36 cm
The perimeter is 36 cm.