Tangent Calculator
Need quick tangent calculations? Our Tangent Calculator makes trigonometry easy! Simply enter an angle (in degrees or radians) and instantly receive the tan(x) value. Whether you're solving homework, engineering problems, or DIY projects, this tool delivers fast, precise results.
Inverse tangent calculator
Share Calculator
About the Tangent Function
The tangent function is one of the six main trigonometric functions and is generally written as tan x. It is the ratio of the opposite side and the adjacent side of the angle under consideration in a right-angled triangle. We have various trigonometric identities and formulas related to the tangent function that can be derived using different formulas. The formula for the period of the tangent function f(x) = a tan (bx) is given by Period = π/|b|. The tangent function tan x is a periodic function and has a period of π/1 = π (because b = 1 in tan x).
How is the Tangent of an Angle Calculated?
The tangent of an angle (tan θ) is calculated using one of these primary methods:
Right Triangle Method
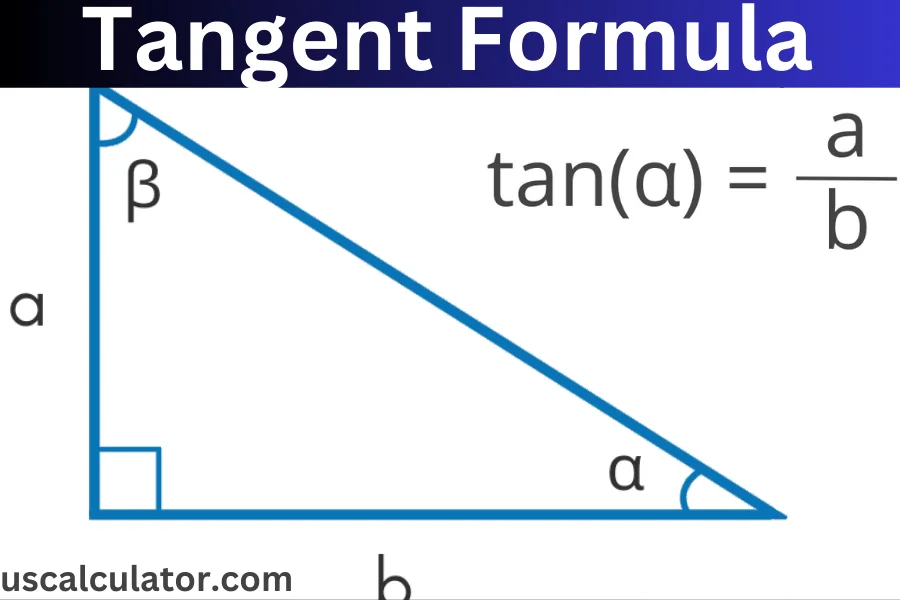
| tan(θ) = | | Opposite Side | | | Adjacent Side |
|
Unit Circle Method
Series Expansion (Advanced)
| tan(x) = x + |
|
+ |
|
+ ⋯ (for x |
+ |
|
) |
Tangent function calculation Formula.
Key Formulas
Basic Definition:
| tan(θ) = | | Opposite Side | | | Adjacent Side |
|
Relationship with Sine/Cosine:
Pythagorean Identity:
1 + tan 2 (θ) = sec 2 (θ)
The tangent of an angle θ in a unit circle, with a radius equal to 1, is calculated by dividing the y-coordinate by the x-coordinate at the point where the angle's terminal side crosses the circle.
For instance, if an angle θ such that tan(θ)=1, this indicates that the opposing side and the adjacent side are equal. This occurs frequently when
θ = π/4 radians or 45 degrees.
In this case, tangentValue represents the tangent of angle θ. Remember that the outcome is the ratio of the lengths represented as a decimal number.
Tangent function calculation Example.
Given: Right triangle with: Opposite side = 3 Adjacent side = 4
1. Identify sides 2: Apply formula
Find angle (optional)
θ = tan -1 (0.75) = 36.87°
How the tangent of an angle is calculated.
Example 1. Let's now use the formula given above to compute the tangent and also understand what the tangent is. Let you have a side of 10 and another side b, which is 15. From these two measurements, you want to determine the angle. If a=10 and b=15 angle a = arctg(10 / 15) = 0.666. Therefore, this angle in this triangle is 0.666
Example 2. Suppose again, for example, you have a right triangle with an adjacent side of 8 units and the opposite side of 6 units. As you remember, the tangent of the angle we need is the ratio of the longest side to the adjacent one, the latter being 8 units long. First, we need to determine which sides are adjacent and opposite. Our opposite side is 6 units, and the adjacent side is 8 units. We plug these numbers into the formula and get Tan(θ) = 6 units / 8 units. Tan(θ) = 3/4. As a result, 3/4 is the tangent of the angle in this triangle.
About the Tangent Function
Properties
| Property | Description |
|---|
| Domain | All real numbers except π/2 + nπ (n ∈ Z) |
| Range | All real numbers (-∞, ∞) |
| Period | π radians (180°) |
| Symmetry | Odd function: tan(-θ) = -tan(θ) |
| Asymptotes | At θ = π/2 + nπ |
Special Values
| Angle (θ) | tan(θ) |
|---|
| 0° | 0 |
| 30° | 1/√3 = 0.577 |
| 45° | 1 |
| 60° | √3 = 1.732 |
| Undefined | Undefined |
common tangent values
| x | tan(x) |
| degrees | radians |
| -90° | -π/2 | not defined |
| -60° | -π/3 | -1.732050808 |
| -45° | -π/4 | -1 |
| -30° | -π/6 | -0.577350269 |
| 0° | π/6 | 0 |
| 30° | π/5 | 0.577350 |
| 45° | π/4 | 1 |
| 60° | π/3 | 1.732051 |
| 90° | π/2 | undefined |
| 120° | 2π/3 | -1.732051 |
| 135° | 3π/4 | 0.707107 |
| 150° | 5π/6 | -0.577350 |
| 180° | π | 0 |
