Cotangent Calculator
Need quick cotangent calculations? Our Cotangent Calculator makes trigonometry simple! Enter any angle (degrees or radians) to get the cot(x) value instantly. Ideal for students, engineers, and math enthusiasts, this is for solving complex problems.
Share Calculator
What is Cotangent?
Cotangent is one of the six basic trigonometric functions and is usually denoted as cot(θ). They are the opposite of one another and can be described as a right triangle or a circle. In easy language, the cotangent of an angle is equal to the side opposite to that angle divided by the side that is adjacent to the tangent of that angle.
Cotangent function calculation formula.
The function of the cotangent, as highlighted
cot is the reciprocal of the tangent function. In a right triangle, it shows the ratio of the length of the adjacent side to the length of the opposite side. Given the angle θ, if x = cot(θ), then x is the cotangent of θ.
formulas: In mathematics: Basic Definition:
| cot(θ) = | | Adjacent Side | | | Opposite Side |
|
Reciprocal Identity:
Pythagorean Identity:
1 + cot 2(θ) = csc 2(θ)
How is the Cotangent of an Angle Calculated?
The cotangent (cot) of an angle is calculated using one of these primary methods:
Right Triangle Method
| cot(θ) = | | Adjacent Side | | | Opposite Side |
|
Unit Circle Method
Relationship with Tangent
Using the formula above, we shall now compute the cotangent. Furthermore, comprehend cotangent. Assume that your a side is 16 long and your b side is 8 long. Using these two measurements, you wish to determine the angle.
If b = 8 and a = 16, tan(α) = 8 / 16 = 0.5.
Thus, this triangle has an angle of 0.5.
Cotangent function calculation Example.
Example Calculation
Given: Right triangle with: Adjacent side = 4 Opposite side = 3
Identify sides and Apply formula
Find angle (optional)
θ=cot -1 (1.333) = 36.87°
About the Cotangent Function Key Properties
| Property | Description |
|---|
| Domain | All real numbers except nπ (n ∈ Z) |
| Range | All real numbers (-∞, ∞) |
| Period | π radians (180°) |
| Symmetry | Odd function: cot(-θ) = -cot(θ) |
| Asymptotes | At θ = nπ |
Special Values
| Angle (θ) | cot(θ) |
|---|
| 30° | √3 = 1.732 |
| 45° | 1 |
| 60° | 1/√3 ≈ 0.577 |
| 90° | 0 |
| 180° | Undefined |
Try It Yourself!
Find cot(30°) using an equilateral triangle (height = √3, base = 1).
Knowledge of the Principal Trigonometric Functions
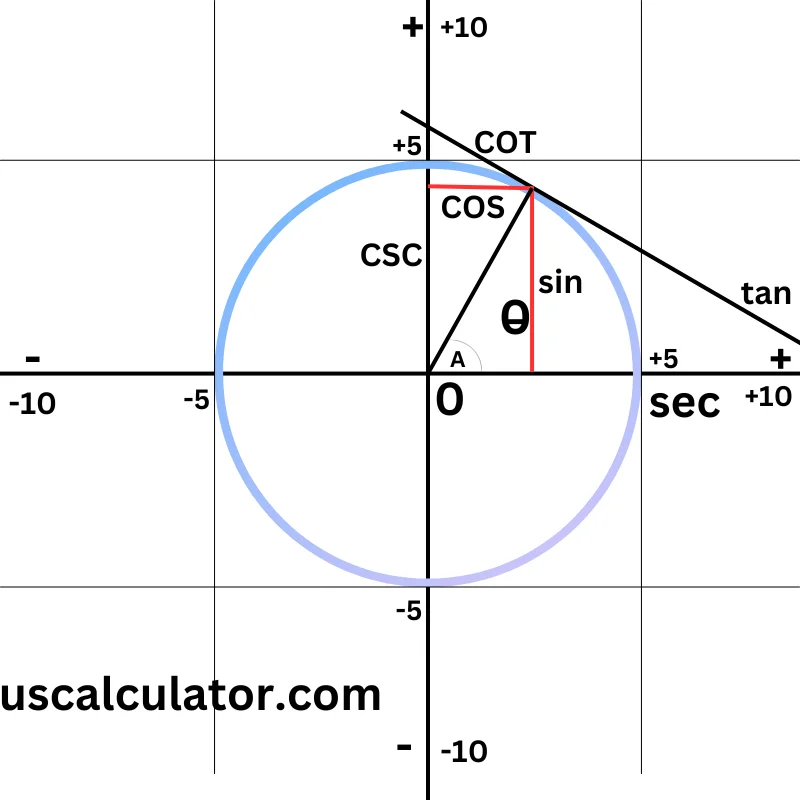
Common Cotangent Values
| Angle (degrees) | Angle (radians) | Cotangent |
|---|
| 0° | 0 | undefined |
| 15° | π / 12 | 2 + √3 |
| 30° | π / 6 | √3 |
| 45° | π / 4 | 1 |
| 60° | π / 3 | 1 / √3 = √3 / 3 |
| 75° | 5π / 12 | 2 - √3 |
| 90° | π / 2 | 0 |
| 105° | 7π / 12 | -2 + √3 |
| 120° | 2π / 3 | -1 / √3 = -√3 / 3 |
| 135° | 3π / 4 | -1 |
| 150° | 5π / 6 | -√3 |
| 165° | 11π / 12 | -2 - √3 |
| 180° | π | undefined |
| 195° | 13π / 12 | 2 + √3 |
| 210° | 7π / 6 | √3 |
| 225° | 5π / 4 | 1 |
| 240° | 4π / 3 | 1 / √3 = √3 / 3 |
| 255° | 17π / 12 | 2 - √3 |
| 270° | 3π / 2 | 0 |
| 285° | 19π / 12 | -2 + √3 |
| 300° | 5π / 3 | -1 / √3 = -√3 / 3 |
| 315° | 7π / 4 | -1 |
| 330° | 11π / 6 | -√3 |
| 345° | 23π / 12 | -2 - √3 |
| 360° | 2π | undefined |
