Arccot Calculator
Need to find an angle from a cotangent value? Our Arccot Calculator (cot⁻¹) makes it easy! Just enter the adjacent/opposite ratio and get the angle instantly in degrees or radians. Ideal for students, engineers, and math enthusiasts.
Share Calculator
How is the arccot of a number calculated?
The arccotangent (arccot) function calculates the angle whose cotangent equals a given number. Unlike arctan, which takes the opposite/adjacent ratio, arccot uses the adjacent/opposite ratio. It's mathematically related to arctan through:
| arccot(x) | | -arctan(x)(for positive x) |
Properties:
Input: Any real number (-∞ to ∞)
Output Range: (0, π) radians or (0°, 180°)
Behavior: Decreasing function (as x increases, arccot(x) decreases)
Arccot function calculation formula.
| θ=cot -1 ( | | Adjacent Side | | | Opposite Side |
| ) |
Arccot function calculation Example.
Example Calculation
Given: A right triangle with: Adjacent side = 4 Opposite side = 3
Compute cotangent ratio
Apply arccot
θ=cot-1 (1.333) = 36.87° or 0.6435 rad
Verification:
Example: use arccot to find an angle
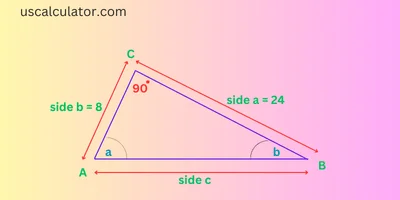
Now, here we understand an example of the use of arccot. To understand this, we have given below a picture of the isosceles triangle. In this figure, we have two sides of known length.
The known side length is a = 24, the hypotenuse is b = 8, and a right triangle is shown at point C.
Now we first divide the opposite side and calculate the cot of a.
This gives cot (a) = b/a = 8/24 = 0.3333.
0Now we will use the inverse function here. Using the inverse function, we get degrees and radians. a = arccot (0.3333) = 71.556° (1.2490 radians).
How Calculators Compute Arccot
Most calculators use the identity:
| cot -1 (x) = tan -1 ( | | ) | (for x > 0) |
For negative inputs:
| cot -1 (x) = π + tan -1 ( | | ) | (for x < 0) |
Example:
cot -1 (2) = tan -1 (0.5) = 26.565°
About the Arccot Function
Key Characteristics
| Property | Details |
|---|
| Domain | All real numbers (x ∈ R) |
| Range | (0, π) radians or (0°, 180°) |
Special Values
cot -1 (0) = 90°
cot -1 (1) = 45°
cot -1 (√3) = 30°
Symmetry
cot -1 (-x) = π - cot -1 (x)
Arccot vs. Arctan
| Feature | Arccot(x) | Arctan(x) |
|---|
| Input Ratio | Adjacent/Opposite | Opposite/Adjacent |
| Primary Range | (0, π) rad | (-π/2, π/2) rad |
| Behavior | Decreasing | Increasing |
| At x = 1 | 45° | 45° |
