Cosine Calculator
To quickly get the cosine of an angle given in degrees or radians, use our Cosine Calculator. In geometry issues involving circles, right triangles, and other shapes where cos(x) may be computed, the cosine is used.
Share Calculator
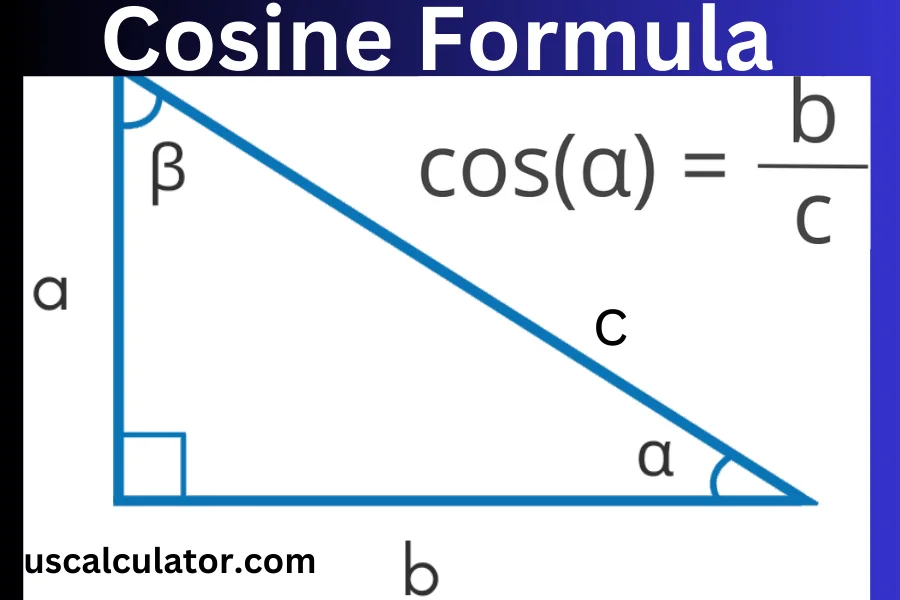
How is the Cosine of a Number Calculated?
The cosine of an angle is calculated using the ratio of the adjacent side to the hypotenuse in a right-angled triangle. For any angle θ:
Calculation Right Triangle Method: Measure sides and compute ratio
Unit Circle Method: x-coordinate on unit circle
Series Expansion (Advanced):
Calculator/Software: Uses optimized algorithms
Cosine function calculation formula.
Key Formulas
Right Triangle Formula:
Unit Circle Formula:
cos (θ) = x - coordinate
Pythagorean Identity:
sin2 (θ) + cos2 (θ) = 1
Cosine function calculation Example.
Given: Right triangle with: Adjacent side = 4 Hypotenuse = 5
1: Identify sides 2: Apply formula
Find angle (optional) θ = cos -1 (0.8) = 36.87°
We will now calculate the cosine function based on the formula given above. And understand cosine. Suppose you have an adjacent triangle with the adjacent side 4 units long and the hypotenuse (the longest side) 5 units long between the two. You want to find the cosine of the angle between the adjacent side (4 units) and the hypotenuse.
We first need to identify the adjacent side and the hypotenuse. Our adjacent side = 4 units, and the hypotenuse = 5 units. Now we plug these values into the formula. So cos(θ) = 4 units / 5 units. cos(θ) = 0.8 cos(θ) = 4 / 5 units. Cos (θ) = 0.8 (this may be expressed as a fraction as well). Thus, 0.8, or 4/5, is the cosine of the angle in this triangle.
If you calculate antilog based on the antilog calculation formula, but have any doubts, use our Cosine calculator to double-check the findings if you're not sure.
About the Cosine Function
Key Properties
| Property | Description |
|---|
| Domain | All real numbers (θ ∈ R) |
| Range | [-1, 1] |
| Period | 2π radians (360°) |
| Symmetry | Even function: cos(-θ) = cos(θ) |
| Zeros | θ = π/2 + nπ (n ∈ Z) |
Special Values
| Angle (θ) | cos(θ) |
|---|
| 0° | 1 |
| 30° | √3/2 = 0.866 |
| 45° | √2/2 = 0.707 |
| 60° | 0.5 |
| 90° | 0 |
Understanding Cosine
Cosine Function (cos(x)): Cos(x), the cosine function, helps us to further comprehend angles. It gives an indication of the relationship between the angles of a right triangle in a way that is close to a handy calculator.
Related Trigonometric Functions: Before we delve straight to finding the cosine, we need to be acquainted with sine, sin(x), and tangent, tan(x). As a group, they form the so-called trigonometric functions triad. To learn the mysteries of angles, they join hands.
How to Calculate an Angle's Cosine: We can therefore see that if we have to find the cosine of an angle, we would not have a problem getting it. It turns out that there is an easy way to achieve all that, and here’s the formula. Take an angle and apply the cosine of it, and voilà! The result lay between -1 and 1 as a value. As the angle increases, the outcome approaches -1 or 1, and this feature is desirable while computing machine learning algorithms.
Uses for the Cosine Function: Now, you might ask why cos(x) is useful and appeals to practical purposes. Others extend it beyond purely arithmetical terms; it is applicable in almost every field of study.
Cosine Calculator for Triangles: Finding Sides and Angles
The basic cosine ratio applies naturally in the case of right triangles:
cos(θ) = adjacent / hypotenuse
Knowing one angle and one side gives you the ability to calculate the other one, whereas knowing two sides is enough to determine the angle by using the reverse cosine function.
Let’s look at an example of a right triangle: a ladder leaning against the wall. The length of the ladder is 10 feet (the hypotenuse), and the base of the ladder is 6 feet away from the wall (the adjacent side).
cos(θ) = 6 / 10 = 0.6
θ = arccos(0.6) = 53.13°
As for the non-right triangles, one should apply the law of cosines:
c² = a² + b² – 2ab cos(C)
or rearranged to find an angle:
cos(C) = (a² + b² – c²) / (2ab)
The next step is to take the inverse cosine. Various online cosine calculators possess a triangle mode that can take the three sides and give the three angles, or take the two sides and the angle between the two sides and find the third side.
This is very helpful in surveying, construction layout, and navigation problems where most triangles are not right triangles.
Degrees vs Radians: Choosing the Correct Mode for a Cosine Calculator
Most problems in schools and daily activities are solved in degrees. 360° is a full circle.
In contrast, more complex mathematics, including calculus and several formulas in physics, requires the use of radians. In terms of radians, a complete circle is equal to 2π, or about 6.2832.
Here are simple conversion formulas:
Degrees = Radians × (180 / π)
Radians = Degrees × (π / 180)
An ideal cosine calculator allows for a switch between the modes with a single click, or provides the answers in both. If the problem states nothing about the units, degrees are assumed as the default unless the context of the problem is mathematics or programming (where radians are usually used in most languages).
Frequently Asked Questions: Cosine Calculator Related Queries
1. What is the value of cosine for angle 0 degrees?
The value is exactly 1. As the angle value approaches 0, the adjacent side is equal to the hypotenuse.
2. How to calculate angle value using cosine calculator?
One needs to input cosine value (between -1 and 1) and select the inverse cosine function or arccos function. It is important to ensure that the mode of measurement selected is same as desired unit, degrees or radians.
3. Is it possible to calculate angle using cosine calculator in radians?
Yes. One needs to set calculator in radian mode, and then either add the angle in radians or enter cosine value.
4. What is the range of arccosine?
Most of the calculators give range from 0 to 180 degrees (or 0 to pi).
5. Is the cosine positive or negative in quadrants?
Cosine values are positive in first quadrant and negative in second and third quadrant. Cosine is again positive in fourth quadrant.
Common Cosine values table
| x (deg) | x (rad) | sine(x) |
| 0° | 0 | 1 |
| 30° | π/6 | 0.866025 |
| 45° | π/4 | 0.707107 |
| 60° | π/3 | 0.50 |
| 90° | π/2 | 0 |
| 120° | 2π/3 | -0.50 |
| 135° | 3π/4 | -0.707107 |
| 150° | 5π/6 | -0.866025 |
| 180° | π | -1 |
Cosine Table
| Angle (degrees) | Angle (radians) | Cos X |
|---|
| 0° | 0 | 1 |
| 15° | π / 12 | √6 + √2 / 4 |
| 30° | π / 6 | √3 / 2 |
| 45° | π / 4 | √2 / 2 |
| 60° | π / 3 | 1 / 2 |
| 75° | 5 π / 12 | √6 - √2 / 4 |
| 90° | π / 2 | 0 |
| 105° | 7 π / 12 | - √6 - √2 / 4 |
| 120° | 2 π / 3 | - 1 / 2 |
| 135° | 3 π / 4 | - √2 / 2 |
| 150° | 5 π / 6 | - √3 / 2 |
| 165° | 11 π / 12 | - √6 + √2 / 4 |
| 180° | π | - 1 |
| 195° | 13 π / 12 | - √6 + √2 / 4 |
| 210° | 7 π / 6 | - √3 / 2 |
| 225° | 5 π / 4 | - √2 / 2 |
| 240° | 4 π / 3 | - 1 / 2 |
| 255° | 17 π / 12 | - √6 - √2 / 4 |
| 270° | 3 π / 2 | 0 |
| 285° | 19 π / 12 | √6 - √2 / 4 |
| 300° | 5 π / 3 | 1 / 2 |
| 315° | 7 π / 4 | √2 / 2 |
| 330° | 11 π / 6 | √3 / 2 |
| 345° | 23 π / 12 | √6 + √2 / 4 |
| 360° | 2 π | 1 |
