Tangent Calculator
Need quick tangent calculations? Our Tangent Calculator makes trigonometry easy! Simply enter an angle (in degrees or radians) and instantly receive the tan(x) value. Whether you’re solving homework, engineering problems, or DIY projects, this tool delivers fast, precise results.
Share This Tangent Calculator
Related Calculators
About the Tangent Function
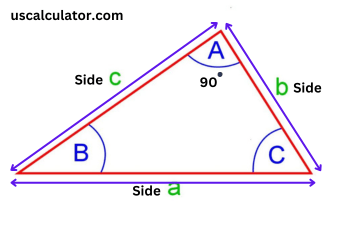
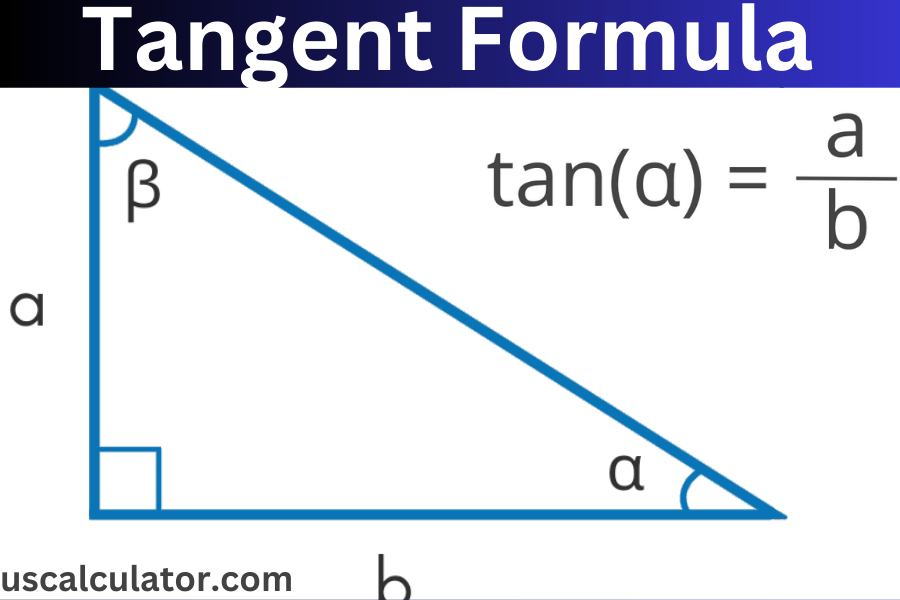
The tangent function is one of the six main trigonometric functions and is generally written as tan x. It is the ratio of the opposite side and the adjacent side of the angle under consideration in a right-angled triangle. We have various trigonometric identities and formulas related to the tangent function that can be derived using different formulas. The formula for the period of the tangent function f(x) = a tan (bx) is given by Period = π/|b|. The tangent function tan x is a periodic function and has a period of π/1 = π (because b = 1 in tan x).
Tangent function calculation formula .
tengent formula: In mathematics
tan(θ)=Adjacent SideOpposite Side
Alternatively, the tangent function can be expressed in terms of sine and cosine:
tan(θ)=cos(θ)sin(θ)
The tangent of an angle is calculated.
Example 1. Let’s now use the formula given above to compute the tangent and also understand what the tangent is. Let you have a side of 10 and another side b, which is 15. From these two measurements, you want to determine the angle. If a=10 and b=15 angle α = arctg(10 / 15) = 0.666. Therefore, this angle in this triangle is 0.666
Example 2. Suppose again, for example, you have a right triangle with an adjacent side of 8 units and the opposite side of 6 units. As you remember, the tangent of the angle we need is the ratio of the longest side to the adjacent one, the latter being 8 units long. First, we need to determine which sides are adjacent and opposite. Our opposite side is 6 units, and the adjacent side is 8 units. We plug these numbers into the formula and get Tan(θ) = 6 units / 8 units. Tan(θ) = 3/4. As a result, 3/4 is the tangent of the angle in this triangle.
Frequently Asked Questions (FAQ)
1. What is the thing called tangent when the angle is 0 degrees?
The tangent of 0 degrees is 0. This is so since the opposite side length in a right-angled triangle is zero each time the angle is equal to 0 degrees.
2. What is the reason that the tangent of 90 degrees is undefined?
The tangent of 90 degrees is undefined because the argument involves division by zero. In a right-angled triangle, the adjacent side becomes zero, and hence it gives an undefined value at 90 degrees.
3. I want to know the circumstances when to use radians as well as when to use degrees.
Serve degrees for the majority of actual geometric problems and normal measurements of angles. Radians are used in calculus, trigonometry, and physics because they are much easier to work with than degrees.
4. Does the tangent calculator work with negative angles?
Indeed, most of the tangent calculators available on the Web are capable of accommodating both positive and negative angles. The tangent function is periodic, and if an angle is negative, the value of the tangent is the same as the value obtained for the positive angle in the opposite direction.
5. What are the real-life uses of the tangent function?
Tangent is applied in navigation, engineering, physics, and the fields of computer and graphic design. It is used in computing gradients and inclinations, phase and frequency, and in the design of circuits that require oscillatory relationships.
6. Indeed, one might naturally wonder: What is the difference between tangent, sine, and cosine?
Tangent, sine, and cosine are all trigonometric functions that relate the angles of a triangle to the lengths of its sides.
Sine (sin θ) = Perpendicular/ Hypotenus
Cosine (cos θ) = adjacent side ÷ hypotenuse
Tangent (tan θ) = (the side opposite to the angle)/(the side next to the angle)
Tangent can also be expressed as the ratio of sine to cosine: tanθ = sinθ / cosθ.
7. Do you ask yourself if the tangent calculator can accept values such as 150 or 300 degrees?
Yes, the tangent calculator is able to process even simple angles as well as complex ones, like angles greater than 90 degrees. It is effective in calculating the tangent of any angle within the reach of the calculator without any errors.
8. Can I find the value of the tangent manually in my hand without any help from a calculator?
Yes, you can use the formula:
tanθ = sinθ / cosθ
If you have to find the tangent of an angle by hand, you will also need the sine and cosine of the same angle. With those, all you need to do is divide the sine of that said angle by the cosine of the same angle.
Tangent Function
common tangent values
| x | tan(x) | |
|---|---|---|
| degrees | radians | |
| -90° | -π/2 | not defined |
| -60° | -π/3 | -1.732050808 |
| -45° | -π/4 | -1 |
| -30° | -π/6 | -0.577350269 |
| 0° | π/6 | 0 |
| 30° | π/5 | 0.577350 |
| 45° | π/4 | 1 |
| 60° | π/3 | 1.732051 |
| 90° | π/2 | undefined |
| 120° | 2π/3 | -1.732051 |
| 135° | 3π/4 | 0.707107 |
| 150° | 5π/6 | -0.577350 |
| 180° | π | 0 |