Greatest Common Divisor Calculator (GCD)

This Greatest Common Divisor Calculator (GCD) calculates the quick Greatest Common Divisor for a set of numbers.

Enter four numbers (one per row):

Calculation results

Document

Share This Calculator

Related Calculators

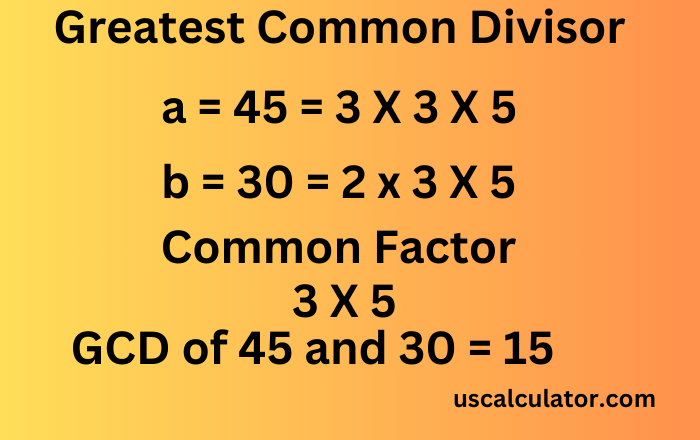
What is Greatest Common Divisor (GCD)?

In this section, we hope to let us understand what is the GCD as well as its name which is the greatest common divisor. Furthermore, it is also called the greatest common factor (GCF) highest common factor (HCF), the greatest common divisor (GCD) greatest common measure (GCM), or the highest common divisor (HCD). A great common divisor (sometimes GCD) is the largest integer among all of the integers that all divide them without leaving no integer. Another name for it is the highest common factor (HCF), or greatest common factor (GCF).

Methods to Calculate GCD

There are three different methods for calculating GCD; these methods are listed below.
1. Prime Factorization Method
2. Division (or Euclidean) Algorithm
3. Binary GCD Algorithm (Stein’s Algorithm)
We will understand 3 ways here and calculate in 3 ways.

1. Prime Factorization Method

Here, we will calculate GCD by the prime factorization method.

First, we will find the prime factorization and make a list of the prime factors of each number.

Now, we will identify the common factors and determine the common factors.

We will multiply the common factors, and multiply the common factors to get GCD.

Let us find the GCD of 48 and 180, for example.

Prime factors of 48: $2^{4} \times 3$

$2^2 \times 3^2 \times 5$

$2^2$

$2^2 \times 3 = 4 \times 3 = 12$

$So,$ 48 and 180 GCD are 12 .

2. Euclidean Algorithm

Here we will calculate GCD by the Euclidean algorithm.

Here we understand the Euclidean algorithm. The Euclidean algorithm is based on the principle that the GCD of two numbers divides their difference as well. We have given below the steps to perform the calculation.

The bigger number will be replaced with the remaining after the larger number has been divided by the smaller number. This procedure will be repeated until the remaining equals zero. The GCD is the non-zero remainder that comes right before this step.

Take an example, we will find the GCDs of 48 and 180.

180 ÷ 48 = 3 remainder 36

48 ÷ 36 = 1 remainder 12

36 ÷ 12 = 3 remainder 0

So, 48 and 180 GCD are 12

Example 1: GCD of 56 and 98

98÷56=1 remainder42

56÷42=1 remainder 14

42÷14=3 remainder 000GCD is 14.

Example 2: GCD of 270 and 192

270 ÷ 192 = 1 remainder 78

192 ÷ 78 = 2 remainder 36

78 ÷ 36 = 2 remainder 6

6 ÷ 6 = 6 remainder 0

The GCD is 6.

Now we will calculate practical Greatest Common Divisor based on the calculation formula.

Presently we will calculate the Greatest Common Divisor based on the calculation formula.

Example 1 (Euclidean Calculation): Identify the prime factorization of both 18 and 30.

Divide 30 (bigger number) by 18 (smaller number): 30 ÷ 18 W 1 leftover portion 12.

Divide 18 by 12 (modern littler number): Thus: 18; while 12 leaves 1 leftover portion 6.

Divide 12 by 6: 12 ÷ 6 = 2 : 0 leftover portion Opposite Impaired.

The last great circular division index is the GCD, which stands for the last non-zero remainder, and it is 6.

Example 2 (Listing Common Divisors): Find out the greatest common divisor of 12 and 20.

List the variables of 12: 1, 2, 3, 4, 6, 12.

List the components of 20: 1, 2, 4, 5, 10, 20.

The closest common factors that appear in both records are 4

We have given the calculation equation of the Most prominent Common Divisor Calculation in a picture over.