Area of a Triangle Calculator for Quick Calculations

Area of a Triangle Calculator

Use this Area of a Triangle calculator to easily calculate the area of a triangle by the all type different possible pieces of information.

Area of a Triangle Calculator

Select units:

Enter side c:

Enter height:

sine

Share This Calculator

Related Calculator

About the Area of a Triangle

This is the formula for a triangle: base * height divided by two. Whatever the triangle is, whether it is an equilateral triangle, a scalene triangle, or a right-angled triangle—that is, whatever the triangle is, if we are given a base or a height in a triangle then we can calculate the area of any triangle by writing the values of all of them in this formula, no matter which triangle it is. So now we know what the base is and what the height is, okay? Because without understanding this, we cannot calculate the area of a triangle. So look, the base is the length of one side of a triangle; we call it the base. A triangle has three sides, so whenever you are given a triangle, we call the bottom side the base. Now let’s understand the height here. What is the height? You guys understand carefully that the base is the line that makes an angle of 90 degrees. That line is up to the top of the triangle; we call it the height.

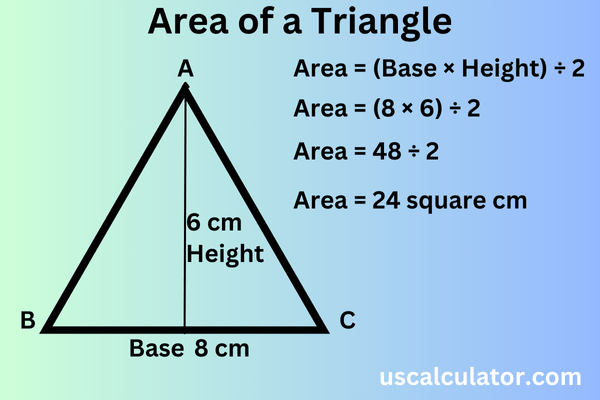
The area of triangle ‘ABC’ is equal to base * height divided by two. So we will write 8 in place of base and then 6 in place of multiplied height. Now let’s solve this: 8 × 6 = 48. Now we will divide 48 by two. What will be the result? 2 × 48 = 24. So the answer, which came out to be 24, will not be the same. So you people should know one rule: whenever you calculate the area of any area, use this metric of area. It always comes square; there are two components. In this, the base and height are in centimeters. Write centimeters here, then write two components on it. So this is the answer, which means it is necessary to write centimeters square. If the height is 6 meters and the base is 8 meters, that is, both are meters, then we write meters here, then divide it by two components. Okay, so in this way, the area of this triangle comes to be 24 centimeters square.

Area of a Triangle Calculation Formula

How can we calculate the area of the square here? Let us understand the process. The size of a rectangle is the same as the space inside it. It tells you how much area the square covers on a flat surface. You get it by using the length of the sides of the triangle and a simple formula.
You can use this handy chart to find the size of a rectangle:
The “base” is the bottom side, and the “height” is the distance from the base to the top corner. Just write these values into a formula, and you get an answer.
Area = (position × elevation) ÷ 2

Area of a Triangle Calculation example

Now, we will calculate the area of the triangle based on the formula above. Simple and easy. Let’s take an example. If the base of a triangle is 6. units and the height is 8. units, you can write these into the formula to find the area: Area = (6 × 8) ÷ 2 (48) ÷ 2 = 24 square units.
Now, if you have a triangle whose sides are 3, 4, and 5 units long, you can use Heron’s formula.

Area of a Triangle Calculation (SSS) side-side-side

Formula All side -The area of a triangle with all three sides given (SSS) can be calculated using Heron's formula -

$Area = \sqrt{� (� - �) (� - �) (� - �)}$

$�$ , $�$ , and $�$ are the lengths of the three sides.
$�$ is the semi-perimeter, calculated as $\frac{� + � + �}{2}$ .

Calculation Example - Let's say we have a triangle with side lengths $� = 5$ , $� = 7$ , and $� = 8$ units. The semi-perimeter would be $� = \frac{5 + 7 + 8}{2} = 10$ units. Plugging these values into the formula:

$Area = \sqrt{10 (10 - 5) (10 - 7) (10 - 8)}$ $= \sqrt{10 \times 5 \times 3 \times 2}$ $= \sqrt{300}$ $\approx 17.32 square units$

Area of a Triangle Calculation SAS (Side-Angle-Side)

Formula SAS - The area of a triangle with two sides and the included angle given (SAS) can be calculated using the following formula:

$Area = \frac{1}{2} \times � \times � \times \sin (�)$

$�$ and $�$ are the lengths of the two sides.
$�$ is the angle between the given sides.

Calculation Example: Consider a triangle with side lengths $� = 6$ and $� = 8$ units, and an included angle $�$ of $4 5^{\circ}$ . Plugging these values into the formula:

$Area = \frac{1}{2} \times 6 \times 8 \times \sin (4 5^{\circ})$ $= \frac{1}{2} \times 6 \times 8 \times \frac{\sqrt{2}}{2}$ $= 24 \times \frac{\sqrt{2}}{2}$ $= 12 \sqrt{2} square units$

$=$ 16.970563 units2

Area of a Triangle Calculation SSA (Side-Side-Angle)

SSA Formula: There can be ambiguity in solving triangles using SSA, leading to two possible triangles or no triangle at all. If a triangle exists, the area can be calculated using the formula:

$Area = \frac{1}{2} \times � \times � \times \sin (�)$

$�$ and $�$ are the lengths of the two given sides.
$�$ is the angle opposite to the side $�$ .

Calculation Example - Suppose we have side lengths $� = 4$ and $� = 5$ units, and an angle $�$ of $3 0^{\circ}$ . Using the formula:

$Area = \frac{1}{2} \times 4 \times 5 \times \sin (3 0^{\circ})$ $= \frac{1}{2} \times 4 \times 5 \times \frac{1}{2}$ $= 10 \times \frac{1}{2}$ $= 5 square units$

Area of a Triangle Calculation ASA (Angle-Side-Angle)

ASA Formula: If two angles and the included side are given (ASA), the area can be calculated by finding the height of the triangle corresponding to the given side and using the formula:

$Area = \frac{1}{2} \times � \times ℎ$

$�$ is the length of the given side.
$ℎ$ is the corresponding altitude or height of the triangle.

Calculation Example: Consider a triangle with side length $� = 10$ units and angles $� = 3 0^{\circ}$ and $� = 6 0^{\circ}$ . We need to find the height corresponding to side $�$ , let's say it's $ℎ = 8$ units. Then:

$Area = \frac{1}{2} \times 10 \times 8$ $= 40 square units$

These formulas and examples should help you navigate the world of triangle areas, no matter what information you're given!

FAQ

1. Is this Area of the Triangle calculator usable for every triangle?

Yes, as long as the base and height are known, the Area of a Triangle Calculator applies to any type of triangle. The theorem is true for scalene, isosceles, and equilateral triangles.

2. What measuring units are permissible?

Any standard measuring units are acceptable, such as meters, feet, inches, centimeters, etc. Square units, whichever is appropriate, will be used to indicate the answer.

3. For what reason is determining the area of the triangle important?

The area of a triangle is critical to a range of activities involving the quantity of materials needed for construction, land area, or other engineering calculations.

4. But what if I only know the triangle’s side lengths?

In that scenario, you will need to use an alternative formula, such as Heron’s formula, or use one of the specialized calculators to find the area by entering the side lengths.

5. How accurate is an area of a triangle calculator’s area?

Depending on the data entered, the Area of a Triangle Calculator displays the precise findings without any further approximation. This feature makes it less prone to any mistakes that could possibly arise from hand calculation.