Area of a Trapezoid Calculator for Quick Calculations

Area of a Trapezoid Calculator

Use this Area of a Trapezoid calculator to easily and quickly calculate the area of a trapezoid given its bases and height.

Area of a Trapezoid Calculator

Select Unit:

Base 1:

Base 2:

Height:

sine

Share This Calculator

Related Calculator

How to Use the Area of a Trapezoid Calculator

We will enter base 1, base 2, and height in the input fields of the calculator. Now we will click on the “Calculate” button, to get the area of the trapezoid immediately. In just a few seconds, the calculator gives us the exact measurement by displaying the calculated area.

About the Area of a Trapezoid (Trapezium)

Here we are going to read about an important topic. Today we will read about trapezium. What is a trapezium, how do you find its area, what is the formula to find its area, and how was that formula made? We will also read its derivation. So first of all, let us try to know what a trapezium is. We have created a trapezium diagram in the image below. To understand this example, see the photo given below.
You must have heard what a quadrilateral is. A closed figure with two sides is now called a quadrilateral. So this is a four-sided figure and is also closed. So this is a quadrilateral, but this is a special type.

Now what is so special about this is that the one on the opposite side of the one on the opposite side means AB and DC are visible to you on one side. So we have made it parallel. One on the opposite side is parallel. So AB and DC, this one on one side will be parallel, and on the other side, visible like AD and BC here, will be non-parallel. Okay, first of all, we have to remember this condition: parallel on one side and non-parallel on the other side. And these parallel sides are called bases. I have taken the upper CD as base 1 and the lower AB as base 2. We have taken the length of the base as b1. Now we have taken the length of B2 between the two parallel lines. In the distance, we have to take the height of the trapezium, and whenever we take the height of the trapezium, we take the perpendicular distance.

We take the perpendicular distance between the two parallel lines. Draw a vertical line from point D, and let’s tell you what this distance is. And the main height of the trapezium is this: You don’t need to draw the perpendicular line from C. If you draw a perpendicular from any point in the middle of the line, all the distances will remain equal, and the main height will remain even because the perpendicular distance in two parallel lines is cm from every point. So b1 is B2, and this height is h. Now, let us understand the formula. What is the formula to find its area? Area of the trapezium ABCD

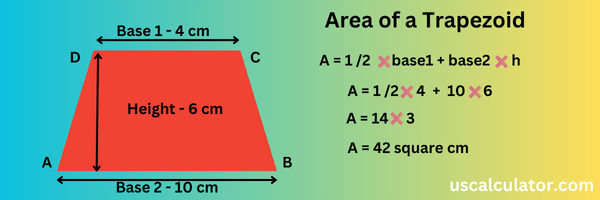
So we have B1 and B2, and this is the height. Now let’s understand the formula to find its area. What is the formula for the area of trapezium ABCD? Area of A = 1/2 × base 1 + base 2 × h. The two bases are b1 and b2. What is the sum of the lengths of parallel lines? Now here, let us assume that DC is 4 cm. Let us assume AB is 10 cm and height H is 6 cm. So these are our dimensions. Now, to find out the area of trapezium, we have the formula. Area = 1/2 × (4+10) × 6. Now, after counting, the area will be 14 × 3. Now we will multiply 14 by 3. So, the area will be 42 square cm.

About the Area of a Trapezoid Calculator

When we have to calculate any area, the first thing we have to do is understand the shape of that area. Here we know how to calculate the area of a trapezoid. Without the proper tools, calculating the area of a trapezoid can be challenging. Fortunately, the area of a trapezoid calculator makes this process easy. Whether working on a construction project in the real world or solving a homework problem, this tool makes it easy to get the area of any trapezium.

Area of a Trapezoid Formula

We have given a formula below, which makes it very easy to calculate the area of a trapezoid. The formula for finding the area (A) of a parallelogram when given both bases and the height is:

$� = \frac{{base}_{1} + {base}_{2}}{2} \times height$

Area of a Trapezoid Calculation Example

Now, we will calculate and understand the area of trapezium calculation based on the formula above.

If the lengths are given as follows:

base1=200 cm base2=100 cm, and height = 150 cm. You can substitute these values into the formula:

$� = \frac{200 + 100}{2} \times 150$

Now, calculate the area:

$� = \frac{300}{2} \times 150$

$� = 150 \times 150$

$� = 22, 500 {cm}^{2}$

So, the correct area of a parallelogram with base1 = 200 cm, base2 = 100 cm, and height = 150 cm is 22,500 cm2. I hope you understand very well.

FAQ

Q: What are the advantages of using an Area of a Trapezoid Calculator rather than calculating all the numbers on one’s head?

A: Performing the calculations to the area of a trapezoid by hand is time-consuming, and any absence of accuracy is likely. Making corrections is fast and the calculator delivers accurate results in the shortest time possible.

Q: Is it capable of performing calculations regarding different units of measure?

A: Absolutely! You can even input your measurements in any units you prefer (for instance, inches, centimeters, or feet), and the Area of a Trapezoid Calculator will convert them for operation.

Q: Can the calculator be used in the learning process?

A: Absolutely! It’s helpful for geometry lessons for students or anyone trying to find the area of a trapezoid quickly.