Area of a Parallelogram Calculator
Do you need to find the area of a parallelogram? Our free calculator makes it easy! Just input the base and height, and get results instantly. Whether for homework, teaching, or quick checks, our tool ensures accuracy with zero hassle.
About the Area of a parallelogram
You will learn how to find the area of a parallelogram here. What is a parallelogram? We have given the shape of a parallelogram to the picture. Any quadrilateral whose opposite sides are equal and parallel is called a parallelogram. So a parallelogram is one in which these are equal to each other and also parallel. Apart from this, a parallelogram has many forms, meaning a rectangle is also a type of parallelogram because in a rectangle, the opposite sides are equal and parallel; these are equal to each other and also parallel. So basically, a rectangle is also a type of parallelogram, but there is a difference in finding its area.
To understand this example better, we have given the image of a parallelogram below.
We have a parallelogram. Its side A is 20 cm, and its side C is 10 cm. We cannot find its area. Remember that if you know the sides of a parallelogram, side A is 20 cm, side B is 20 cm, side C is 10 cm, and side D is 10 cm. Now we know all four sides. Even then, we cannot find its area. So, knowing all four sides of a parallelogram, its area cannot be found. In a rectangle, it is different if side A is 20 cm and side C is 10 cm; then its area will quickly become 20 * 10, and this is 200 square centimeters. So, the area of a parallelogram cannot be found in this way. Now, how is the area of a parallelogram found? Let us understand this. To find the area of a parallelogram, we must have the base and height, so the area of the parallelogram can be found quickly.
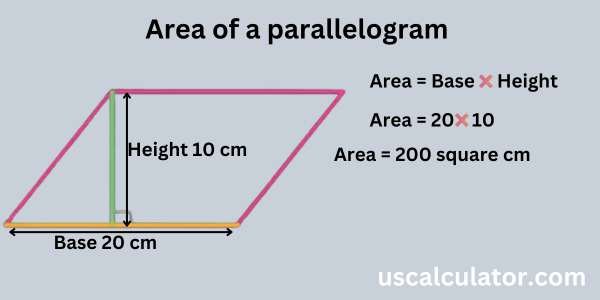
We have a parallelogram; the length and height are given, and the area will be base × height. Area = base × height. Now we have a base of 20 cm and a height of 10 cm. In the formula for the area of a parallelogram, we write area = 20 × 10. So if we count here that the base is 20 and the height is 10, it will be 200 cm square because both are in centimeters. Area = 200 square centimeters.
Area of a parallelogram Calculation formula
We have given a formula below, which makes it very easy to calculate the area of a parallelogram. It’s very simple. The formula for finding the area (A) of a parallelogram is given by –
A = base × height

Area of a Parallelogram Calculation Formula
Now here we will calculate and understand the area of parallelogram calculation based on the formula given above. If the base of the parallelogram is given as 200 cm and the height is given as 100 cm, you can substitute these values into the formula:
A = 200 × 100
Now, calculate the area:
A = 20,000 cm square
So, the area of a parallelogram with a base of 200 cm and a height of 100 cm is 20,000 cm square.
Note - Area of a Parallelogram Calculation
Two measurements are needed; the base can be easily taken, but the height requires forming a right angle with one of the angles of the parallelogram. Whichever side of the angle is the base, it matters.
Next, you can use the following basic multiplication formula, just make sure that both lengths have the same unit of measurement.
The Area of a Parallelogram Calculator
Knowing how to compute a shape’s area is essential while studying geometry. The parallelogram is one of these forms that is easily recognized by its unique pattern of two pairs of parallel sides that have equal opposing angles. It can occasionally be difficult to calculate its area. This is when the Area of a parallelogram calculator for the area of a parallelogram comes in useful. By utilizing simple inputs like base and height, this online tool streamlines the process and enables users to rapidly and reliably calculate the area of a parallelogram.
FAQ
1. What units are expressed by the Area of a Parallelogram Calculator?
The Area of a Parallelogram Calculator can process any unit so long as the base and height are measured in the same unit. Regardless of whether it is meters, centimeters, feet, inches, or any other unit, the area will be expressed in units of area of the same nature.
2. Is height always at a right angle to the base?
Indeed, for uncertainty control when calculating the area, the height must always be the distance perpendicular to the base and the side of the parallelogram.
3. Sometimes the calculator can be used on 3D shapes, but most often only formulas for areas and volumes are provided, which is not enough when working with 3D shapes.
No, this Area of a Parallelogram Calculator is specifically created to work with 2D parallelogram shapes only. For volumes of other three-dimensional geometrical figures like a parallelepiped, a different formula and a different Geometry Tool would be required.
4. Are we allowed to input decimal values for the base and height of the triangle?
Yes, the calculator works for whole numbers or for decimal values as you wish. It will give an area according to any point if referential measurements are required.
5. What if they are skewed or irregular?
Loosely put, as long as what you have is a shape with two pairs of parallel sides, the calculator will work fine. The one critical feature is that the true perpendicular height must be entered.