Harmonic Mean Calculator: Compute Your Values Easily

Harmonic Mean Calculator

Use this harmonic mean calculator. easily calculate the harmonic mean of a set of numbers. Enter the numerical values in the box above.

Harmonic Mean Calculator

Enter numbers (separated by commas)

Calculation results

Harmonic Mean: 0

SHare This Calculator

Related Calculators

A Harmonic Mean: What Is It?

Let us understand the harmonic mean, The harmonic mean is a measure of central tendency, similar to the arithmetic mean (average), but with a different approach. It considers the interrelationships of data points and then takes the average of those interrelationships of data points. In simple terms, it gives more importance to smaller values in a data set. There are three Pythagorean rules. This is one of the three rules. And it gives us the most accurate average. When to use it: Harmonic mean is ideal when you want to find average speed, rate of work, efficiency, or any scenario where small values significantly affect the result.

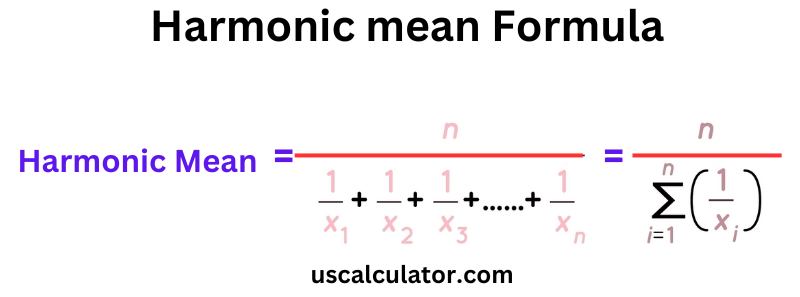
Harmonic Mean Formula

The harmonic mean (H) of n numbers x₁, x₂, ..., xₙ is calculated using the formula:

$� = \frac{�}{\frac{1}{�_{1}} + \frac{1}{�_{2}} + . . . + \frac{1}{�_{�}}}$

How to Calculate the Harmonic Mean

let’s take an example: If you want to find the harmonic mean of the following numbers: 5, 3, 8,.

Let’s say you have a data set with travel times for three different routes (in hours):

Route A: 5 hours

Route B: 3 hours

Route C: 8 hours

To find the harmonic mean travel time,

Calculate the reciprocals: 1/5, 1/3, and 1/8.

Sum the reciprocals: 1/5 + 1/3 + 1/8 ≈ 0.655

Divide the sum by the number of data points (3): 0.655 / 3 ≈ 0.218.

Take the reciprocal of the result: 1 / 0.218 ≈ 4.58.

Therefore, the harmonic mean travel time is approximately 4.58 hours. This value is closer to the slower Route B (3 hours) compared to the arithmetic mean (average), which would be closer to the middle value.

If you calculate Harmonic Mean Based on the Harmonic Mean calculation formula but have doubts, use our Harmonic Mean Calculator to double-check the findings if you’re unsure.

How to Calculate the Harmonic Mean of Two Numbers

For two numbers, x and y, the harmonic mean is:

$� = \frac{2 � �}{� + �}$

Harmonic Mean of Three Numbers

For three numbers, x, y, and z, the harmonic mean is:

$� = \frac{3 � � �}{� � + � � + � �}$

What is the Harmonic Mean Calculator

The Harmonic Mean Calculator is a straightforward tool for calculating the Harmonic Mean. Entering the base number and number is required. It displays the answer in Harmonic Mean, which makes calculating the Harmonic Mean easier.

The Harmonic Mean Calculator primarily aims to simplify Harmonic Mean calculations. Whether you operate as an engineer, businessperson, student, or in another field, it is useful for calculating the Harmonic Mean. In this manner, you can save time and choose the best solutions.

Harmonic Mean vs Arithmetic Mean

Table

Harmonic mean	Arithmetic Mean
Example: 3, 4, 2, 7 n = 4 HM = 4 / (1/3 + 1/4 + 1/2 + 1/7) = 3.2621	Example: 3, 4, 2, 7 n = 4 AM = (3 + 4 + 2 + 7) / 4 = 4
In order to determine this, we take the reciprocal of that data set's reciprocal terms' arithmetic mean.	We divide the total number of observations by the sum of all the observations in a data collection in order to compute this.
Out of the three means, it has the lowest value.	Out of the three means, it has the highest value.
It cannot be used to a collection of data if the rates are zero or negative.	It can be computed regardless of whether the data collection contains zero, positive, or negative numbers.

Harmonic Mean Vs Geometric Mean

Table

Harmonic mean	Geometric Mean
Example: If we are given a sequence 2, 3, 5, 9. n = 4 HM = 4 / (1/2 + 1/3 + 1/5 + 1/9) = 3.4951	Example: If we are given a sequence 2, 3, 5, 9. n = 4 GM = (2 × 3 × 5 × 9)^1/4 = 4.0536
Divide the total number of phrases by the sum of the reciprocal terms to find the harmonic mean given a data collection.	Finding the geometric mean of a data collection with n terms may be done by multiplying each item by itself and obtaining the n^th root.
It is always worth less than the other two means.	Its value is lesser than the arithmetic mean, but always greater than the harmonic mean.
It is the data set's arithmetic mean after a few reciprocal modifications.	With some log adjustments, it may be compared to the arithmetic mean.