Cotangent Calculator
To quickly get the cotangent of an angle given in degrees or radians, use our Cotangent Calculator. This free trigonometry calculator for cot(x) may be used to solve right triangles, circles, and other numbers.
Share This Calculator
Related Calculators
Table of Contents
What is Cotangent?
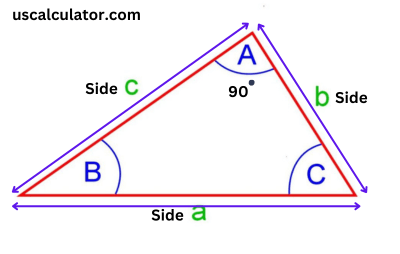
Cotangent is one of the six basic trigonometric functions and is usually denoted as cot(θ). They are the opposite of one another and can be described as a right triangle or a circle. In easy language, the cotangent of an angle is equal to the side opposite to that angle divided by the side that is adjacent to the tangent of that angle.
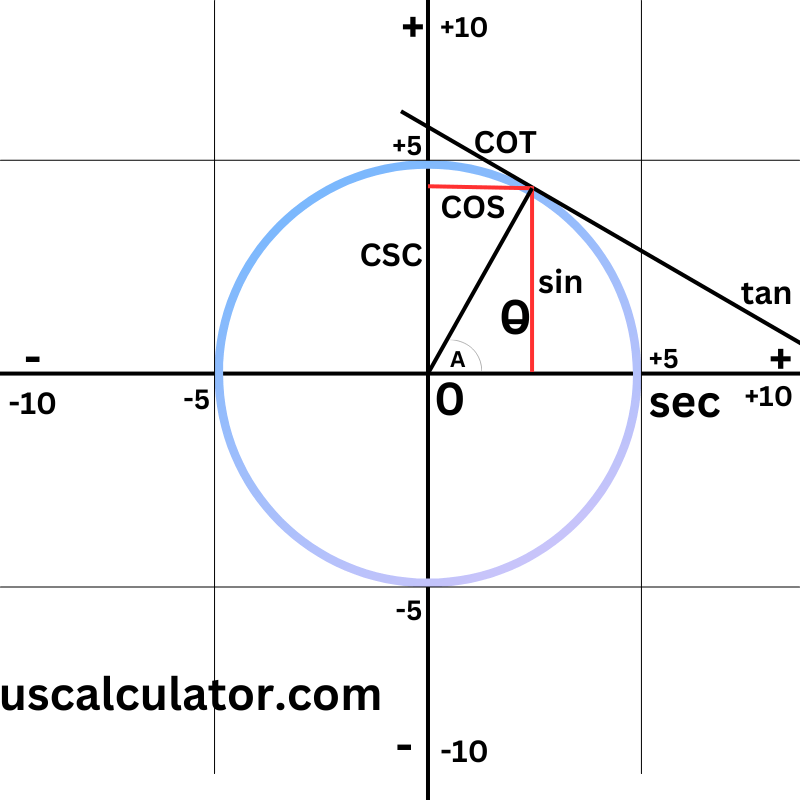
Cotangent function calculation formula .
The function of the cotangent, as highlighted
cot is the reciprocal of the tangent function. In a right triangle, it shows the ratio of the length of the adjacent side to the length of the opposite side. Given the angle θ, if x=cot(θ), then x is the cotangent of θ.
formula: In mathematics:
Alternatively, the cotangent function can be expressed in terms of sine and cosine:
How is the cotangent of an angle calculated?
Using the formula above, we shall now compute the cotangent. Furthermore, comprehend cotangent. Assume that your a side is 16 long and your b side is 8 long. Using these two measurements, you wish to determine the angle.
If b = 8 and a = 16, tan(α) = 8 / 16 = 0.5.
Thus, this triangle has an angle of 0.5.
Knowledge of the Principal Trigonometric Functions
Frequently Asked Questions (FAQ)
1. What is the difference between tangent and cotangent?
Sophisticated product of trigonometry: Tangent (tan) :
dp n=8 and cotangent (cot) (): dp n=8 is a sophisticated product of trigonometry. Tangent means a ratio of the side opposite angle Theta to the side that is next to the angle Theta while cotangent is equal to the reciprocal of Tangent that is equal to the ratio of the side that is next to angle Theta to the side that is opposite angle Theta.
2. What is the cotangent of 45 degrees?
In other words, a cotangent of 45 degrees equals 1. This is because when the angle is 45 degrees, the side opposite to it and the adjacent side in a right triangle are of equal measure and so their ratio cotangent is 1.
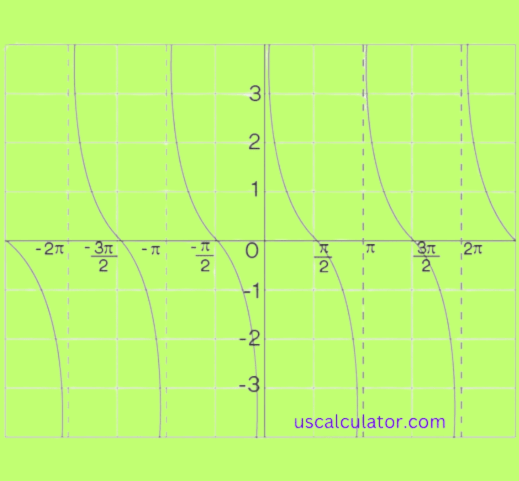
3. When is the cotangent value undefined?
We note that cotangent is equal to the ‘tangent of the angle divided by the angle’; therefore, the cotangent value will be undefined when cos is 0 which occurs when the angle is a multiple of 0°, 180° or π radians. This happens because the sine of these angles is equal to zero and division by zero is not possible in mathematics.
4. What do I need to do to find values of other trigonations in terms of the cot?
You can easily convert cotangent values into other trigonometric functions using these formulas:
cot(θ) = 1 / tan(θ)
cot(θ) = cos(θ) / sin(θ)
5. Can students use the cotangent function within scientific calculators?
Indeed, cotangent is available in most scientific calculators either as a primary function key or as part of a second function linked to one of the keys. However, they are not physical functions on the calculator; to find them, you can use cot(θ)= 1 / tan(θ).
6. Should I be able to solve problems with angles greater than 360 degrees or 2π radians with a cotangent calculator?
Yes, you can. Cotangent is periodic with a period π, so, you can find the cotangent for the greater value of an angle, more than 360° or 2πr, by means of such a reduction.
7. It might be difficult to think of real-world uses of cotangent, but cotangent is used in navigation systems to find the location of lost objects.
Cotangent can be applied in many phases of study for example in physics, engineering, and computer graphics. It finds applications in solving problems involving wave frequencies, signals processing as well as determination of slopes for navigation and construction applications.
cotangent function
common cotangent values
| x | tan(x) | |
|---|---|---|
| degrees | radians | |
| 0° | 0 | undefined |
| 30° | π/6 | 1.732051 |
| 45° | π/4 | 1 |
| 60° | π/3 | 0.577350 |
| 90° | π/2 | 0 |
| 120° | 2π/3 | -0.577350 |
| 135° | 3π/4 | -1 |
| 150° | 5π/6 | -1.732051 |
| 180° | π | undefined |
The arccotangent of a given integer may be quickly calculated with the help of our Arccot Calculator. Allows for the entry of fractions (like 0.5, -0.5).
To quickly get the tangent of an angle expressed in degrees or radians, use our tangent calculator. Right triangles, circles, and other figures involving right-angled triangles with a given angle x from which tan(x) can be calculated can be solved with the help of this trigonometry calculator.
Use this Trigonometry Calculator to easily and quickly calculate trigonometry functions in degrees or radians.