Calculate Area of a Parallelogram with Our Easy Area of a Parallelogram Calculator

Area of a Parallelogram Calculator

Use this Area of a Parallelogram calculator to easily and quickly calculate the area of a parallelogram by its base and height.

Area of a Parallelogram Calculator

Select Unit:

Width:

Height:

Share This Calculator

Related Calculator

About the Area of a parallelogram

You will learn how to find the area of a parallelogram here. What is a parallelogram? We have given the shape of a parallelogram to the picture. Any quadrilateral whose opposite sides are equal and parallel is called a parallelogram. So a parallelogram is one in which these are equal to each other and also parallel. Apart from this, a parallelogram has many forms, meaning a rectangle is also a type of parallelogram because in a rectangle, the opposite sides are equal and parallel, these are equal to each other and also parallel. So basically, a rectangle is also a type of parallelogram, but there is a difference in finding its area.

We have a parallelogram. Its side A is 20 cm, and its side C is 10 cm. We cannot find its area. Remember that if you know the sides of a parallelogram, side A is 20 cm, side B is 20 cm, side C is 10 cm, and side D is 10 cm. Now we know all its four sides. Even then, we cannot find its area. So, knowing all four sides of a parallelogram, its area cannot be found. In a rectangle, it is different that if side A is 20 cm and side C is 10 cm, then its area will quickly become 20 * 10 and this is 200 square centimeters. So, the area of a parallelogram cannot be found in this way. Now, how is the area of a parallelogram found? Let us understand this. To find the area of a parallelogram, we must have the base and height so the area of the parallelogram can be found quickly.

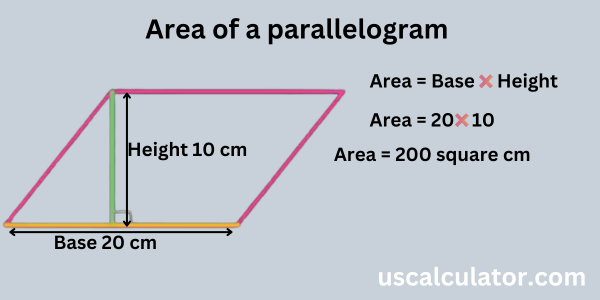
We have a parallelogram; length and height are given, and the area will be base × height. Area = base × height. Now we have a base 20 cm and a height of 10 cm. In the formula for the area of a parallelogram, we write area = 20 × 10. So if we count here that the base is 20 and the height is 10, it will be 200 cm square because both are in centimeters. Area = 200 square centimeters.

Area of a parallelogram Calculation formula

We have given a formula here below, which makes it very easy to calculate the area of a parallelogram. it's very simple . The formula for finding the area ( $A$ ) of a parallelogram is given by -

$� = base \times height$

Area of a Parallelogram Calculation Formula

Now here we will calculate and understand the area of parallelogram calculation based on the formula given above. If the base of the parallelogram is given as 200 cm and the height is given as 100 cm, you can substitute these values into the formula:

$� = 200 \times 100$

Now, calculate the area:

$� = 20, 000$

So, the area of a parallelogram with a base of 200 cm and a height of 100 cm is $20, 000 {cm}^{2}$ .

Note - Area of a Parallelogram Calculation

Two measurements are required; the base may be taken simply, but the height requires making a right angle at one of the parallelogram’s angles. Whichever arm of the angle is the base, that is all that matters.

After that, you may use the following basic multiplication formula, just be sure that both lengths have the same unit of measurement.

The Area of a Parallelogram Calculator

Knowing how to compute a shape’s area is essential while studying geometry. The parallelogram is one of these forms that is easily recognised by its unique pattern of two pairs of parallel sides that have equal opposing angles. It can occasionally be difficult to calculate its area. This is when the Area of a parallelogram calculator for the area of a parallelogram comes in useful. By utilising simple input inputs like base and height, this online tool streamlines the process and enables users to rapidly and reliably calculate the area of a parallelogram.

FAQ

1. What units are expressed by the Area of a Parallelogram Calculator?

The Area of a Parallelogram Calculator can process any unit so long as the base and height are measured in the same unit. Regardless of whether it is meters, centimeters, feet, inches, or any other unit, the area will be expressed in units of area of the same nature.
2. Is height always at a right angle to the base?
Indeed, for uncertainty control when calculating the area, the height must always be the distance perpendicular to the base and the side of the parallelogram.
3. Sometimes the calculator can be used on 3D shapes but most often only formulas of areas and volumes are provided which is not enough when working with 3D shapes.
No, this Area of a Parallelogram Calculator is specifically created to work with 2D parallelogram shapes only. For volumes of other three-dimensional geometrical figures like a parallelepiped, a different formula and a different Geometry Tool would be required.
4. Are we allowed to input decimal values for the base and height of the triangle?
Yes, the calculator works for the whole number or for decimal values as you wish. It will give an area according to any point if referential measurements are required.
5. What if they are skewed or irregular?
Loosely put, as long as what you have is a shape with two pairs of parallel sides the calculator will work fine. The one critical feature is that the true perpendicular height must be entered.